Dr Nicholas Hamilton
To develop new methodologies in machine learning and artificial intelligence to generate useful predictive mathematical models.
Dr Nick Hamilton is the Institute Bio-Mathematician at the Institute for Molecular Bioscience, The University of Queensland, and holds a co-appointment with the Research Computing Centre at UQ.
He gained a PhD in Pure Mathematics from the University of Western Australia in 1996 and was subsequently awarded Fellowships in Australia and Belgium. In 2002, Nick made the decision to change fields into the exciting new areas of computational biology and bioinformatics, returned to Australia, and subsequently took up a position within the ARC Centre of Excellence in Bioinformatics at UQ.
In 2008 he was appointed as a Laboratory Head at IMB, and Institute Bio-Mathematician in 2014, where he continues to lead a group in bio-image informatics, mathematical modelling and data visualisation, developing methodologies to deal with the current deluge of data that new microscopy imaging technologies have enabled.
90 seconds with Dr Hamilton

Dr Nicholas Hamilton
Biomathematician & Senior Research Fellow
+61 7 334 62984
n.hamilton@imb.uq.edu.au
UQ Researcher Profile
The ureteric tree of the kidney is the complex branching structure on which nephrons, the filtering units of the kidney, grow. A research highlight would be the program of research which led to the discovery by my group that the growth of the ureteric tree as it develops follows essentially the same pattern every time. We then found a set of simple mathematical rules that described that pattern of growth. The rules turned out to be similar to the Fibonacci / Golden Ratio rules that can often be found in nature such as in the patterning of shells and sunflowers.
The following image represents the pattern of 6 stages of early growth of the ureteric tree.
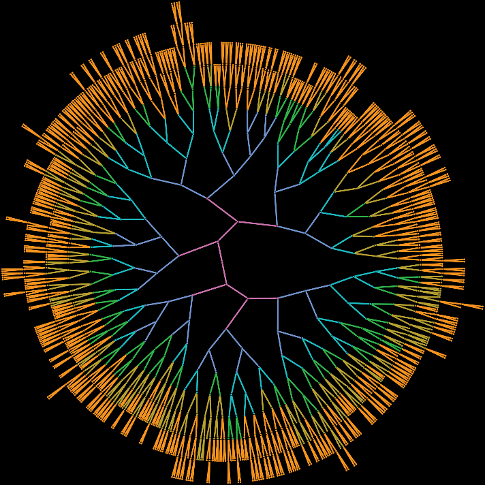
References
J. Lefevre, T.O. Lamberton, K.M. Short, O. Michos, D. Graf, I.M. Smyth, N.A. Hamilton. Branching morphogenesis in the developing kidney is governed by rules that pattern the ureteric tree. Development 144:4377-4385 (2017).
T. Lamberton, J. Lefevre, K.M. Short, I.M. Smyth, N.A. Hamilton. Comparing and distinguishing the structure of biological branching. Journal of Theoretical Biology 365(21):226-237 (2015).
A.N. Combes, K.M. Short, J. Lefevre, N.A. Hamilton, M.H. Little, I.M. Smyth. An integrated pipeline for the multidimensional analysis of organ development. Nature Protocols 9(12):2859-2879 (2014).
K.M. Short, A.N. Combes, J. Lefevre, A.L. Ju, K.M. Georgas, T. Lamberton, O. Cairncross, B.A. Rumballe, A.P. McMahon, N.A. Hamilton, I.M. Smyth, M.H. Little. Global quantification of tissue dynamics in the developing mouse kidney. Developmental Cell 29:188-202 (2014).
How did you get into research?
I was inspired to go to university having read about physicists in the early 20th Century mapping out quantum mechanics in the coffee shops of Copenhagen. The idea of discovering the structure of the universe with back and forth discussion and equations over coffee, sounded very exciting. I have been a dedicated coffee drinker ever since.
Research interests
Mathematical Modelling, Machine Learning, Data Visualisation, Kidney Development, Cell Biology, Bio-Imaging, Cancer Imaging.
Ultimate goal for your research
To use mathematical modelling to discover the nature of fundamental biological processes such as cell protein trafficking and development, which can then ultimately be translated into real world applications in the biomedical field.
Future focus
The second wave of data from the genome revolution is now arriving in the emerging field of high-throughput microscopy imaging of biological molecules in their cellular and organ contexts, live in real time and in high resolution 3D. With terabytes of imaging being generated in a matter of minutes, current analysis methodologies are being overwhelmed. The focus of my group’s research will be to develop new methodologies in machine learning and artificial intelligence to extract meaning from this wealth of imaging data and hence generate biologically useful predictive mathematical models of the systems being observed.
